
Een vreemde weergave van het weer van de laatste 101 jaar waarbij alle gemiddelde etmaal temperaturen op een glijdende schaal zijn gesorteerd maar waarbij gekeken word naar het aantal etmalen verschil die er tussen 2 naast elkaar gelegen temperaturen zijn.
bv. 14-2-1929 is met -15,4°C net iets kouder dan 1-1-1997 met -14,9°C (en er bestaat nog geen datum waarop er een temperatuur was die tussen deze beide etmalen past), maar het tijdsverschil tussen beide is 67,88020792 jaar.
De sequentie van de tijdsverschillen is relatief tov. de absolute datums die gekoppeld zijn aan de volgorde van het etmaalgemiddelde op de glijdende schaal van temperatuur en deze wijzigt zich met elke nieuwe etmaal en zijn gemeten etmaalgemiddelde.
Zo worden de naastgelegen datums van 31-12-1998 dus 23-11-1961 en 27-10-1958
en de naastgelegen datums van 1-1-1999 worden dan 8-11-1961 en 21-4-1982 louter omdat hun temperaturen van het etmaalgemiddelde elkaar direct in lijn opvolgen.
De bovenstaande grafiek toont al die tijdsverschillen als een histogram met 101 kolommen. De kans dat een etmaal binnen 1 jaar naast het etmaalgemiddelde van vandaag valt (omdat het gelijk is, een iets kleiner danwel groter is dan het etmaalgemiddelde van vandaag) is hetzelfde als de kans dat er tussen twee naast elkaar gelegen etmaalgemiddelden 1 jaar of kleiner tijdsverschil bestaat en dat is 825/37026≈1/45≈2,23% van alle gemeten dagen.
Stats C:
0 jaarfractie
N 37026
Min 0,00273224
Max 100,984
Sum 1,24236E06
Mean 33,5537
Std. error 0,124679
Variance 575,563
Stand. dev 23,9909
Median 29,2693
Skewness 0,565423
Kurtosis -0,611411
Geom. mean 21,8884
Opmerkelijk genoeg zijn er tijdsverschillen die minder frequent voorkomen (zie in bovenstaande afbeelding de rode kolommen) dan de verwachting mag zijn.
De kans dat twee naast elkaar gelegen temperaturen een tijdsverschil hebben in de orde van 5 jaar is lager dan de ernaast gelegen tijdsverschillen. Dit geldt ook voor
de ordes van 20 jaar, 33 jaar, 61 jaar en 83 jaar
Het wijst op een (significant?) patroon?
Er is natuurlijk een voorkeur, nl. de kans is groter dat twee temperaturen dichter bij elkaar liggen als er niet meer dan 3 maanden tijdsverschil tussen is.
Voor het eerste jaar is de kans ongeveer 349/825 (≈42,3% van alle jaardagen) dat de temperatuur van twee etmaalgemiddelden ongeveer dezelfde waarde hebben als er niet meer dan 3 maanden tijdsverschil tussen beide temperaturen liggen.

Opmerkelijk genoeg daalt diezelfde kans mee met het aantal jaren dat ertussen ligt (zie bovenstaande afb. met 404 kolommen).
Het verschil in frequentie tussen 1 kwartaaltijdsverschil vgl. met een halfjaartijdsverschil en ook met 9 maandentijdsverschil is wel te begrijpen, aangezien we dan de lente met de herfst of winter zouden vergelijken etc.
Ook hier is het aantal malen dat twee opeenvolgende temperaturen een tijdsverschil van 100 jaar hebben vele malen kleiner dan dat twee opeenvolgende temperaturen een tijdsverschil van 1 jaar of kleiner hebben.
Er zijn 8 datums tussen 1906 en nu die een tijdsverschil met de ernaast gelegen datum hebben die groter is dan 100, hiervan zijn er 4 met jaargang 1906.
Er zijn 814 datums tussen 1906 en nu met een tijdsverschil kleiner dan 1 met de ernaast gelegen datum, hiervan zijn er 8 met jaargang 1906
In excel ziet de histogram van de frequenties met andere kolombreedtes er zo uit:

Er lijkt een cyclus te zijn die zich elke 10 jaar herhaalt, een zonnecyclus?.
Hier zijn dezelfde gegevens nogmaals maar als lijndiagram:

Waarom er echter een verschil is in frequentie tussen een jaarlijks tijdsverschil, welke zelfs omgekeerd evenredig verloopt, ontloopt nadere analyse. We mogen voorlopig vastellen dat hoe groter een tijdsverschil is des te groter de kans is dat er een temperatuur komt die dat verschil breekt. Net zoals bij door het toeval gegenereerde getallen het absoluut verschil tussen elkaar opeenvolgende toevalsgetallen het resultaat uit vele kleintjes en enkele grotere bestaan. Een Qbasic programm laat dit zien:
--------------------------------
dim A(100001)
for k=1 to 100000
Z= int(rnd(1)*100000)+1
A(k)=Z
G= abs(A(k)-A(k-1))
print G
N=N+G
if G<50001 h="H+1:H1="H1+G">50000 then J=J+1:J1=J1+G
next k
print N/100000,H,J,H1,J1
--------------------------------------------------
Het gemiddelde N/totaal aantal worpen zweeft rondom 1/3 van het bereik van het aantal mogelijke toevallige waarden
De frequentie van de getallen kleiner dan de helft+1 van het aantal worpen is 3 keer zo hoog als de frequentie van de getallen groter dan de helft van het aantal worpen, resp. 75%:25%
De som van de partij kleiner dan de helft+1 van het totale bereik van het tijdsverschil is ongeveer gelijk aan de partij groter dan de helft van het totale bereik van het tijdsverschil resp. 50%:50%
Deze getallen vind men ook terug in de duizendbladsteelmethode van de I Ching, en ook de I Ching zelf bestaat uit twee grote stukken, 64 kleinere stukken en 384 hele kleine stukken (maar deze zijn hier wel een deelverzameling van). En ook in het diagram blijkt dat 74,4558% van de tijdsverschillen kleiner of gelijk te zijn aan 50. De verdeling van som van beide partijen blijken ook bijna gelijk te zijn aan elkaar.
Zo hebben de volgende datums (met hun etmaalgemiddelde temp.) een grote kans om in de toekomst in de squentie op te moeten schuiven aangezien hun tijdsverschil met een van hun ernaast gelegen datum groter is dan 100 jaar (indien gesorteerd op etmaalgemiddelde dan op minimum en vervolgens op maximum temp.):
11-12-1906--+8°C
19-2-2007--+5,7°C
3-3-2007--+6,4°C
30-4-1906--+7,2°C
15-6-1906--+10,6°C
1-5-2007--+15,3°C
17-6-1906--+16,2°C
20-8-2006--+16,5°C
Het volgende Qbasic programmaatje toont de voortschrijdende verdeling aan voor iedere
dag dat erbij komt.
---------------------
dim A(10100)
[start]
k=k+1
Z= int(rnd(1)*100)+1
A(k)=Z
G= abs(A(k)-A(k-1))
N=N+G
if G<51 h="H+1:H1="H1+G">50 then J=J+1:J1=J1+G
print k,N/k,H,J,H+J,H1,J1
If k=10000 then end
goto [start]
-----------------------------------
In de het gemiddelde, de frequentie verdeling en de verdeling van de som blijkt dan niets te veranderen.
Zo blijken er nu voor het het 1906 alleen al 186 etmalen te zijn met een tijdsverschil groter dan 50 jaar. Dit is 51% van het aantal dagen van het jaar 1906.
Over de gehele gemeten periode van 101 jaar (37027 etmalen) zijn er 9459 etmalen met een tijdsverschil groter dan 50 jaar.
We weten dat voor 1906 het aantal dagem met een groter tijdverschil dan de helft van het aantal gemeten dagen (dus 365) ook ongeveer 25% moet zijn geweest. Zo blijken er 75 van de 365 dagen in 1906 een tijdsverschil te hebben gehad groter dan 182,5 etmalen. Daarvan blijken 45 etmalen hedentendage nog steeds het predikaat te hebben dat ze een groter tijdsverschil hebben dan 50 jaar. 30 etmalen van 1906 hebben een tijdsverschil met het predikaat dat ze niet meer groter zijn dan de helft van het aantal gemeten etmalen, wat neerkomt op 12% van 365 etmalen. 141 etmalen van 1906 hebben vandaag wel een tijdsverschil groter dan de helft van het aantal gemeten etmalen en in 1906 niet. Het lijkt erop dat er ook een 75% (141/186) kans is dat een tegenwoordig groter tijdsverschil vroeger een kleiner tijdsverschil is geweest.
Hieronder is een afbeelding met het lijndiagram van de tijdsverschillen en nadien in de juiste sequentie naar tijd (1=1-1-1906 en 365=31-12-1906) gezet.

Even terzijde:
Er zijn dus vier soorten tijdsverschillen
kleiner dan helft naar groter dan de helft
groter dan helft naar kleiner dan de helft
kleiner blijft kleiner dan de helft
en groter blijft groter dan de helft
respectievelijk te vergelijken met: oude yin, oude yang, jonge yin en jonge yang.
Sterke lijnen zijn dan tijdsverschillen die nauwelijks gealterneerd hebben tussen kleiner of groter dan de vorige periode. Zwakke lijnen alterneren zeer vaak (herfst/lente?). Op de juiste plaats als het in de zomer zomers was?
Indien we nu ook nog kijken of het boven (yang) of onder (yin) het gemiddelde tijdsverschil van de tijdreeks ligt, kan men de acht trigrammen reconstrueren. Waarschijnlijk was de hele I tjing niet meer dan een weeralmanak.
De matrix hieronder geeft aan hoe het kan, je ziet dat dagen niet altijd hetzelfde tijdsverschil hebben, maar dat tijdsverschillen zeer lang achtereen hetzelfde kunnen zijn op een bepaalde dag. Groen betekent groter dan het halve tijdsverschil tussen de jaren en donkergroen geeft zelfs aan dat het tijdsverschil even groot is als het tijdsverschil met dat bepaald jaar en 1906. Ongeveer 48% ((783+17062)/37229) van alle vakjes zijn groen. En indien een vakje donkergroen is dan is op dezelfde dag een jaar later het tijdsverschil in dat vakje nooit lager dan de helft van het bereik maw. ongebroken. De enige uitzondering hierop is het eerstvolgende jaar (1907) dat volgt op het indexjaar (idg. 1906).
Ongeveer 2,1% van alle vakjes zijn donkergroen maar 8% van alle tijdsverschillen zijn kleiner dan 1.

De getallen worden verkregen door eerst alle dagen te selecteren van 1906 tot en met een bepaald jaar in de volgorde zoals die nu staat (dwz. met hun etmaalgemiddeldde temp. van koud naar warm, ook voor de minimum- en dan maximumtemp.), vervolgens hun tijdsverschillen onderling opnieuw uitrekenen en dan sorteren voor alleen die dagen uit 1906. Na zo'n 100 permutaties met de sequentie (elk jaar eenmaal) blijven de volgende 5 dagen over die ook nu nog dezelfde waarde hebben als in 1906 én kleiner dan 1 zijn en in al die tussenliggende tijd nooit veranderd zijn:
22-feb, 19-maart, 26-september, 4-oktober en 22-oktober. Dit betekent dan hun etmaalgemiddelde temperatuur op die datums vgl. met de ernaastgelegen etmaalgemiddelde temperatuur in de glijdende schaal nooit de waarde van het tijdsverschil veranderde welke het met de ernaastgelegen datum heeft en dus ermee altijd zijn positie zoals vastgelegd in 1906 in de sequentie behield. Er zijn 189 dagen in 1906 waarbij het hetzelfde tijdverschil niet wordt herhaald in de daaropvolgende jaren. Er zij dus 176 dagen waarbij het tijdsverschil dus doorloopt tot in de jaren na 1906 en waarvan er dus 5 (1,3%) nu nog steeds bestaan. De verhouding is ongeveer 50%:50%. (Indien men niet wilt weten wat er van een temperatuur geworden is maar waar het vandaan kwam dient men het hele berekeningsprotocol nog eens te doen maar dan beginnende met het huidige jaar, de verhouding wordt dan 182 dagen -doorlopende- staat tot 183 dagen,zie alhier.
Na verwerking van alle gegevens verkrijgt men de volgende diagram:

En indien er een klimaatcrisis zou zijn zou het dan een mooie curve zijn?
Echter vanaf 1931 is het minimale tijdsverschil 2 dagen en vanaf 1992 is het minimale tijdsverschil plots 9 dagen. Wat overreenkomt met de observatie dat de lente nu ongeveer twee weken eerder begint dan in 1906. Het eerste jaar waarin het grootste tijdsverschil kleiner is dan het tijdsverschil tussen 1906 en dat jaar is 1977.
Indien men de trend van de blauwe reeks uit bovenstaande grafiek doortrekt heeft over 90 jaar geen enkel jaar met 1906 nog een tijdsverschil dat kleiner dan 1 jaar is.
Het bestand is hier online te zien (excel 97-2003) of hier te downloaden:DivShare File - vegl-time2.xlsb (binair XLS bestand--office 2007 bestand)
Waarom niet gewoon etmaalgemiddelde temperaturen met elkaar vergeleken ipv. de verschuiving van tijdsverschillen met 1906? Omdat men aan de tijdsverschillen kan zien of zo'n vergelijk enige betrouwbaarheid heeft en met alleen etmaalgemiddelde niet. Zo blijkt de grafiek over de som van de percentielen er zo uit te zien:

Elke daling staat voor een vermindering in het aantal dagen met dezelfde tijdsverschillen. In formule: (B/365)+(B/A). Het zweeft netjes rond 1 en het uiteindelijke resultaat is altijd 1+(x/365), waarbij x het aantal rijen zijn die nog doorlopen van idg. 1906 tot nu.
Indien ik de bij alle gemeten gemiddelde etmaaltemperaturen van de laatste 101 jaar elk tijdsverschilletje een aparte kolom geef (weer in Past software) krijgen we het volgende resultaat:
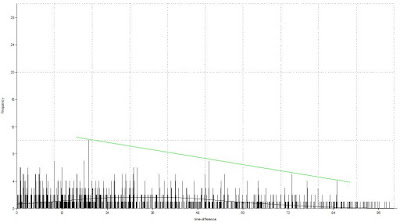
en bij 37026 kolommen verdwijnt het omgekeerd evenredige verband uit de vorige afbeeldingen.
Een zwakke afspiegeling ervan vormen de 4 kolommen die steeds in grootte afnemen en beginnen na 19 jaar en elkaar opvolgen in lengte en tijd langs de groene lijn.
Indien het heden ten dage werkelijk warmer is geworden dan 100 jaar geleden dan zou dat verband ook zichtbaar moeten zijn.
Misschien is hiermee zelfs de werking van het geheugen verklaard, slechts door te zoeken naar dichtsbijzijnde datums die ook binnen een mensenleven vallen kan men keydatums produceren met een hoge connotatie.
Indien de aarde echt warmer wordt betekent dit ook een breuk in het collectieve geheugen aangezien in de toekomst bepaalde temperatuur data niet meer voorkomen en dus ook nauwelijks nog de kans hebben om de tijdsverschillen met de erbij behorende connotatie te triggeren.
Hieronder is een voorbeeld waarbij hetzelfde als in bovenstaande beschreven is gedaan, maar dan van een periode van de laatste 45+ jaar vanaf vandaag waarbij de periode verdeelt is in 180 kolommen.
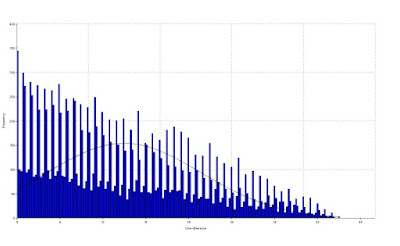
Zo kan men van elke periode, locatie of persoon een tijdsverschillen-profiel maken,
hieronder is een 'fingerprint' van dezelfde periode/persoon als hierboven.

Maar indien ik van elke dag het verschil (afgerond in jaren) opteken tussen de tijdsverschillen met dezelfde dag het jaar ervoor en van elk jaar op zich het gemiddelde van die verschillen uitreken krijg ik de onderstaande diagram over de laatste 101 jaar:

Alleen 1949 heeft een gemiddeld verschil dat groter is dan 1 jaar
Het gemiddelde over de 101 jaar is 0,513
De eerste 33 jaar is het gemiddelde 0,482, de middelste 33 jaar heeft een gemiddelde van 0,519 maar de volgende 33 jaar is het gemiddelde 0,546. Dit vormt bijna een stijgende rechte lijn.
Het verschil tussen de tijdsverschillen wordt dus steeds groter.
Dit is echter schijn want een diagram van de gemiddelde verschil van elke decade na 1906 ziet er zo uit:

Het verschil tussen de eerste decade (06-16) en de negende decade (86-96) is maar liefst 0,162 groot en het grootste verschil zit tussen de 8ste en 9de decade, dat zou (al) kunnen wijzen op een klimaatcrisis?
Ook hier blijkt dat we nog te weinig gegevens hebben. Er is zelfs nog onvoldoende bewijs dat het einde van de wereld op 21 december 2012 enig effect op het klimaat zal hebben. Evenmin is er enig bewijs dat de veronderstelde klimaatcrisis katastrofaal voor de aarde is.
Tel ik het werkelijk aantal tijdsverschillen (niet afgerond!) per dag per jaar ongelijk aan het voorafgaande jaar dan krijg ik het volgende diagram:

Met een som van 2123 en een gemiddelde van 5,82 over de hele periode 1906-nu.
Dan heeft de nazomer/herfst duidelijk de grootste amplitude en de winter de kleinste amplitude.
Het komt echter slechts maar 5 maal voor in de periode 1906-nu dat in een gegeven jaar op twee opeenvolgende dagen de tijdsverschillen gelijk aan elkaar zijn: 1 maal in 1906, 3 maal in 1907 en 1 maal in 1908 op 7 aug, 28 okt en 24 november.
Wat dus even nietszeggend is.
Waarschijnlijk is de hele klimaatcrisis niet meer dan een rekenblunder door tegenwoordige weerfeiten te vergelijken met de weerfeiten van 100 jaar geleden waarbij statistich gezien eigenlijk alles (nog) mogelijk blijkt.
Klimaat is namelijk het gemeten gemiddelde over een periode van 30 jaar in een bepaald gebied. Theoretisch zijn we sinds 1906 al 3 klimaten verder en halverwege onze 4de klimaat.
Volledig normaal dus.
Voor de die-hards onder ons hier is de grafiek vanaf 1906 tot nu met alle etmaalgemiddelde temperaturen (TG) als punten in de grafiek en zijn regressielijn, er is nauwelijks een stijging, de correlatiecoefficient ervan is 0,0046204!!:

en dezelfde grafiek voor de laatste 40 jaar:

laat pas een lichte stijging zien, met een correlatiecoeficient van 0,079349.
Gelukkig heb ik meer verstand van bier.












